
Oltre il Rinascimento a Firenze – La sezione aurea in arte e a Palazzo Rucellai
Questa volta il titolo “Oltre il Rinascimento” va
interpretato come “Rinascimento oltre se stesso”, cioè al culmine della sua
idea del mondo e della riscoperta della cultura classica.
La facciata di Palazzo
Rucellai, progettata da Leon Battista Alberti e completata nel 1465, è celebrata
come una delle opere-simbolo dello spirito dell’epoca. L’Alberti la progettò
come una dimostrazione esemplare dei suoi principi architettonici, descritti
nel suo libro De Re Aedificatoria
(Sull’architettura, 1452), per i quali la bellezza non deriva dallo sfarzo o
dalla magnificenza decorativa, ma dall’armonia e dal fascino delle proporzioni.
La facciata, di bugnato aggettante di pietraforte, è strutturata
su tre piani come una griglia regolare di rettangoli, definiti in orizzontale da
cornici marcapiano e alla base dalla panca di via, in verticale da paraste e
lesene con capitelli. Questi rettangoli racchiudono finestre bifore al primo e
secondo piano e finestrelle e portoni a pian terreno. Molti sono gli elementi
tratti dall’architettura classica, ma qui ne vediamo in particolare uno solo,
ma clamoroso: tutti i rettangoli che costituiscono la griglia sono costruiti
sulla base della sezione aurea.
Che cos’è la sezione aurea? Senza entrare nella definizione
matematica, in geometria è la proporzione
particolare tra due segmenti disuguali che possono costituire elementi di
rettangoli, triangoli e pentagoni. Dividendo la misura del segmento grande con
la misura di quello più piccolo si ha il numero irrazionale (cioè che ha
decimali infiniti) 1,6180339887… . Il rettangolo, che ha i lati tra loro in
questa proporzione, era considerato già nel mondo greco-romano il canone “naturale” della bellezza e dell’armonia.
Il Partenone ad Atene è interamente strutturato su questi rettangoli “aurei”, gli stessi che costituiscono la
facciata di Palazzo Rucellai.
La sezione aurea ha una lunga storia. La sua definizione
risale al VI secolo A.C. ed è attribuita a Pitagora e ai suoi discepoli che gli
davano significati magici e astrologici. I greci erano convinti che le opere costruite
su queste proporzioni davano un forte senso di ordine, armonia e simmetria. Un
senso di compiutezza e di perfezione in cui intravedevano un disegno divino,
uno schema superiore utilizzato dagli dei per creare la natura, l’uomo e
l’universo. Anche Platone gli dava un significato mistico e affermava: Dio geometrizza sempre. Anche il corpo
umano, per essere “bello”, doveva
essere perfettamente simmetrico e con proporzioni “auree”.
Gli artisti del Rinascimento erano affascinati da questa
armonia dell’arte antica. Il manuale “De Architectura”, opera di Vitruvio - un
architetto romano del I secolo A.C che
era stato sovrintendente alle macchine da guerra nell’esercito di Cesare e
architetto di corte di Augusto - era stato tradotto dall’umanista Poggio
Bracciolini nel 1414. Il libro, molto amato da Lorenzo Ghiberti, Leon Battista
Alberti, Raffaello, Paolo Giovio e altri, impressionò in particolare Leonardo
da Vinci.
Vitruvio aveva studiato le basi “matematiche” della bellezza del corpo umano, stabilendo che
l’altezza deve essere uguale all’apertura delle braccia e che la figura può
essere iscritta in un cerchio. Su questa base aveva poi calcolato le misure
proporzionali “perfette” di tutte le parti del corpo. Ispirato da Vitruvio,
Leonardo nel 1490 disegnò il famosissimo Uomo
vitruviano, l'uomo ideale, che è stato per secoli alla base degli
studi di estetica anatomica. La figura è inserita in un cerchio (il cielo) e in
un quadrato (la terra). Il raggio del cerchio è la sezione aurea del lato del
quadrato. Leonardo ricalcolò anche tutte le proporzioni delle parti del corpo
umano “perfetto” fatte da Vitruvio, confermandole, ad eccezione dei piedi
che secondo lui dovevano essere più corti: un settimo dell’altezza, invece del
sesto calcolato da Vitruvio.
Il disegno di Leonardo è diventato uno dei simboli dell’Umanesimo
e del Rinascimento. Il cerchio e il quadrato sono figure geometriche
“perfette”. L’uomo, proporzionato sulla sezione
aurea, è stato creato perfetto perché è al centro dell’universo e, come si
diceva, è “artefice della propria sorte”,
può gestire la propria vita, può scegliere il proprio destino. Il contrario
dell’uomo medioevale, schiacciato dalla divinità.
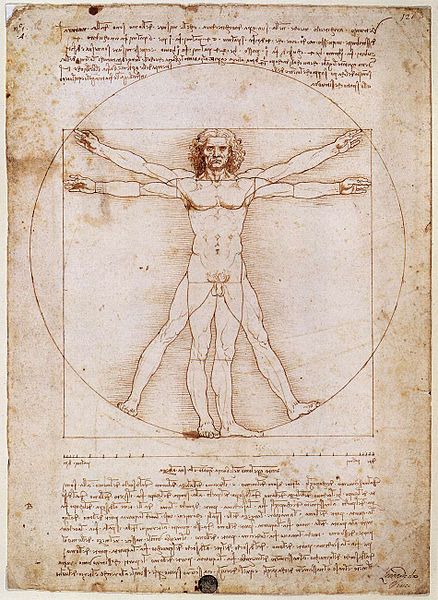
L'Uomo Vitruviano di Leonardo Da Vinci.
Leonardo usò la sezione aurea anche nella pittura, come nell’Ultima
Cena e nel volto della Gioconda. Molti altri
artisti se ne sono serviti, incluso Le Corbusier, uno dei più importanti architetti del 1900. L’architetto svizzero, teorizzò che, dato che la sezione aurea è alla base
delle proporzioni del corpo umano, tutti gli spazi di
abitazione e di lavoro in cui l’uomo si muove devono essere strutturati su
queste misure. Leon Battista Alberti non era arrivato a tanto.
Perfino Paperino di Walt Disney si ha avuto a che fare con la sezione aurea. Nel cartone animato del 1959 Paperino nel mondo della matemagica (Donald in Mathmagic Land), usato come filmato didattico nelle scuole americane, Paperino entra nel Paese delle Meraviglie della Matematica. Lì incontra Pitagora che sta suonando in una jam session jazz con i suoi discepoli. Il filosofo greco gli svela che il mondo è basato sulla matematica e che la sezione aurea è dappertutto: nella Piramide di Cheope, nella Gioconda di Leonardo, nella Venere di Milo di Alessandro d’Antiochia, nel Partenone di Fidia ad Atene e nel Palazzo dell’ONU a New York di Le Corbusier, nel corpo umano, nella musica, nella struttura dei fiori, degli animali marini, delle galassie. Insomma in ogni forma dell’universo. Paperino, sbalordito, finalmente si convince che il futuro è nella matematica e nella geometria.
Una curiosità: i due lati delle nostre carte di credito, bancomat e ormai ogni
tessera magnetica sono proporzionati sulla sezione aurea. Se dividete il lato
maggiore con quello minore, otterrete sempre 1,6180339887… !
Foto di copertina: la facciata di Palazzo Rucellai.



